所罗门诺夫的宝藏:通用人工智能之路
时间行至 2025 年底,那个曾被视为遥远科幻概念的「通用人工智能」(AGI),如今已不再是空谈,而是成为了摆在每个人案头沉甸甸的现实。
在这个时代,我们目睹了两种截然不同的情绪。一边是深沉的忧虑与克制。图灵奖得主 Geoffrey Hinton 对 AGI 表达了深切的恐惧,甚至坦言后悔自己的研究,担心失控的智能将毁灭人类;而传奇人物 Ilya Sutskever 更是为了追求根本上的安全,毅然建立 SSI(Safe Superintelligence),踏上了一条孤独的道路——去构建一个从根本上安全、可控的超级智能。另一边则是狂热的有效加速主义(e/acc)。他们高呼「加速」,主张不惜一切代价推进技术奇点,坚信算力与智能的指数级爆发将是解决人类所有顽疾的终极解药,任何减速行为都是对文明的犯罪。
然而,在这些关于算力竞赛、安全控制与社会伦理的喧嚣讨论之下,人工智能领域其实一直埋藏着一条草蛇灰线的「暗线」。这条线索早在 40 多年前就已存在,它无关当下的 GPU 集群,也不谈论 Transformer 的层数,而是用最纯粹的数学语言,定义了「智能」的本质。
这条暗线,始于图灵(Turing),成于柯尔莫哥洛夫(Kolmogorov),并在雷·所罗门诺夫(Ray Solomonoff)手中汇聚成一座灯塔。今天,让我们暂时从 2025 年的纷扰中抽身,沿着 Ilya Sutskever 那句著名的「压缩即智能」回溯,去重新发现那座被现代 AI 遗忘的数学宝藏——所罗门诺夫通用归纳(Solomonoff Induction)。
一、智能的本质:从压缩到预测
压缩=寻找规律
让我们先回到传奇人物 Ilya Sutskever 身上。在 2023 年的一次讲座中,Ilya 抛出了一个在当时引起轰动的观点:「智能即压缩」。

这个想法听起来简洁得令人意外,但其背后蕴含着深刻的逻辑:为了压缩大规模的语言数据,或者任何形式的数据,你必须寻找到其中蕴含的规律。你的规律找得越准确、越简单,你就越能够极致地压缩数据。而「寻找规律」的过程,恰恰就是建模的过程。
我们可以想象一个确定性的世界,大语言模型(LLM)的任务是尽可能准确地预测下一个 token。如果在这个世界里,「下一个 token」是完全没有随机性的,那么一个完美的模型不仅能准确预测未来,也能完美地压缩过去——你只需要给出一段极短的提示词(Prompt),模型就能利用它所掌握的规律,精准地还原出整篇文章。
事实上,早在 2016 年,OpenAI 内部就已经萌生了这种思想的雏形。但很多人不知道的是,如果从「压缩即智能」这一概念继续上溯,我们会发现它连接着算法信息论的三位祖师爷:Hutter 的 $AI\xi$、所罗门诺夫的通用归纳,以及大名鼎鼎的 Kolmogorov。
时间序列:万物的统一视角
为了真正理解这套理论,我们需要打破传统机器学习中「训练」与「推理」泾渭分明的界限。在生物智能中,观察、学习与预测是交织在一起的流。为了描述这种过程,我们必须引入时间 $t$,构建一个统一的图像:一切智能活动,本质上都是基于过去的观测 $x_{1:t}$,来预测下一时刻 $x_{t+1}$。
在这个框架下,$x_{1:t}$ 就是我们所有的「经验」。这个 $x_t$ 的形式极其灵活:它可以是一串数字,那么你在做时间序列预测;它可以是一张图像的像素流,那么你在做生成式建模;它甚至可以是「图像-标签」的配对序列,给定图像 $x_t$,去预测标签 $x_{t+1}$,那么你就在做分类任务。
由此可见,这种抽象的时间序列视角,实则蕴含了机器学习中的万千法门。而所有任务的核心,都归结为一个条件概率:
$$ p(x_{t+1} \mid x_{1:t}) = \frac{p(x_{1:t+1})}{p(x_{1:t})} $$这个公式告诉我们,要预测未来($x_{t+1}$),本质上等同于要能够评估整个序列($x_{1:t+1}$)发生的概率。换句话说,谁能最准确地计算出一段数据出现的先验概率,谁就掌握了预测未来的钥匙。
奥卡姆与伊壁鸠鲁的博弈
既然目标明确,那我们该如何预测?让我们玩一个简单的「找规律」游戏。假设有这样一串数字:
$$ 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, \dots $$如何预测下一个数字?在这个问题面前,人类的直觉往往会分裂成三种哲学态度:
第一种是奥卡姆剃刀(Occam’s Razor)。这是人类直觉的首选。你会敏锐地发现「两个 1 之间的 0 每次增加一个」这个简单的规律。根据这个规律,接下来应该是四个 0,然后是 1。我们偏爱它,因为它简单。
第二种是不可知论(或者说是阴谋论)。你可以争辩说,这串数字只是从一个更大的、完全不同的序列中截取的片段。也许在下一个数字之后,规律会突变,变成全都是 1。虽然这听起来很别扭,但在数据出现之前,你无法从逻辑上证伪它。
第三种是纯粹的随机性。也许这是一串完全随机的数字,之前的规律纯属巧合,就像看着云彩像一只羊一样,只是我们的错觉。
这就引出了古希腊哲学家伊壁鸠鲁(Epicurean)的**「多重解释原则」**:「凡经验允许多种解释者,皆当并存,而非独断。」这意味着,虽然我们偏爱简单的解释(奥卡姆),但我们不能武断地抛弃其他复杂的可能性,除非新的证据彻底否定了它们。
这似乎是一个两难的困境:奥卡姆剃刀要求我们只选最简单的,而伊壁鸠鲁要求我们保留所有的。如何将这两者统一起来?

「那些只执一种解释的人,是在与事实相冲突的。」—— Diogenes Laertius《哲学家列传》第十卷 - 致皮托克勒书 -伊壁鸠鲁
所罗门诺夫归纳,正是这两个看似矛盾的原则在数学上的完美联姻。
二、数学的神谕:从算法概率到通用归纳
要理解所罗门诺夫的伟大之处,我们不能简单地认为他是一个把哲学翻译成公式的翻译官。恰恰相反,他是一个探索者。他试图回答一个最根本的问题:在这个宇宙中,一段数据 $x$ 出现的先验概率到底是多少?
如果我们能算准这个先验概率(记为 $M(x)$),根据贝叶斯公式,我们就能完美地预测未来。雷·所罗门诺夫并没有凭空设计一个公式,而是从一个思想实验出发,推导出了那个惊人的结论。
算法概率 $M$:猴子与打字机的数学真相
让我们想象那个著名的场景:一只猴子在键盘上随机敲打。但在所罗门诺夫的版本里,猴子敲的不是诗句,而是二进制代码,输入给一台通用的图灵机。
如果不做任何假设,我们唯一知道的真理是:**程序的生成服从随机过程。为了数学严谨,我们需要引入前缀码(Prefix-free Code)**的概念(即机器读到一段完整代码就会停机执行,不会读成另一段代码的前缀)。如果猴子随机且独立地敲击 0 或 1,那么一个长度为 $|p|$ 的特定程序被敲出来的概率,精确地等于 $2^{-|p|}$。
现在,我们要问:这只猴子敲出的程序,运行后输出结果恰好是数据 $x$ 的概率是多少?
显然,这是所有能够输出 $x$ 的程序概率之和,我们称之为算法概率(Algorithmic Probability),记为 $M(x)$:
$$ M(x) = \sum_{p:U(p)=x} 2^{-|p|} $$这里出现了一个并非人为设计的、而是数学上必然的结果:由于这是一个 $2$ 的负指数求和,总和的数值将由那个最短的程序主导。
这就引入了柯尔莫哥洛夫复杂度 $K(x)$——即输出 $x$ 的最短程序长度。
$$ K(x) := \min_{p} \{ |p| : U(p) = x \} $$举个例子,假设生成数据 $x$ 的最短程序长度是 100 位,次短的是 200 位。$2^{-100}$ 是 $2^{-200}$ 的 $2^{100}$ 倍!后面那些冗长、复杂的程序,对总概率的贡献微乎其微。
因此,我们得到了一个震撼的近似:
$$ M(x) \approx 2^{-K(x)} $$这正是奥卡姆剃刀的真正来源。 奥卡姆剃刀并非人类为了省事而发明的主观偏好,它是算法世界的物理定律:越简单的东西($K$ 小),被算法随机生成的概率($M$)就越大。
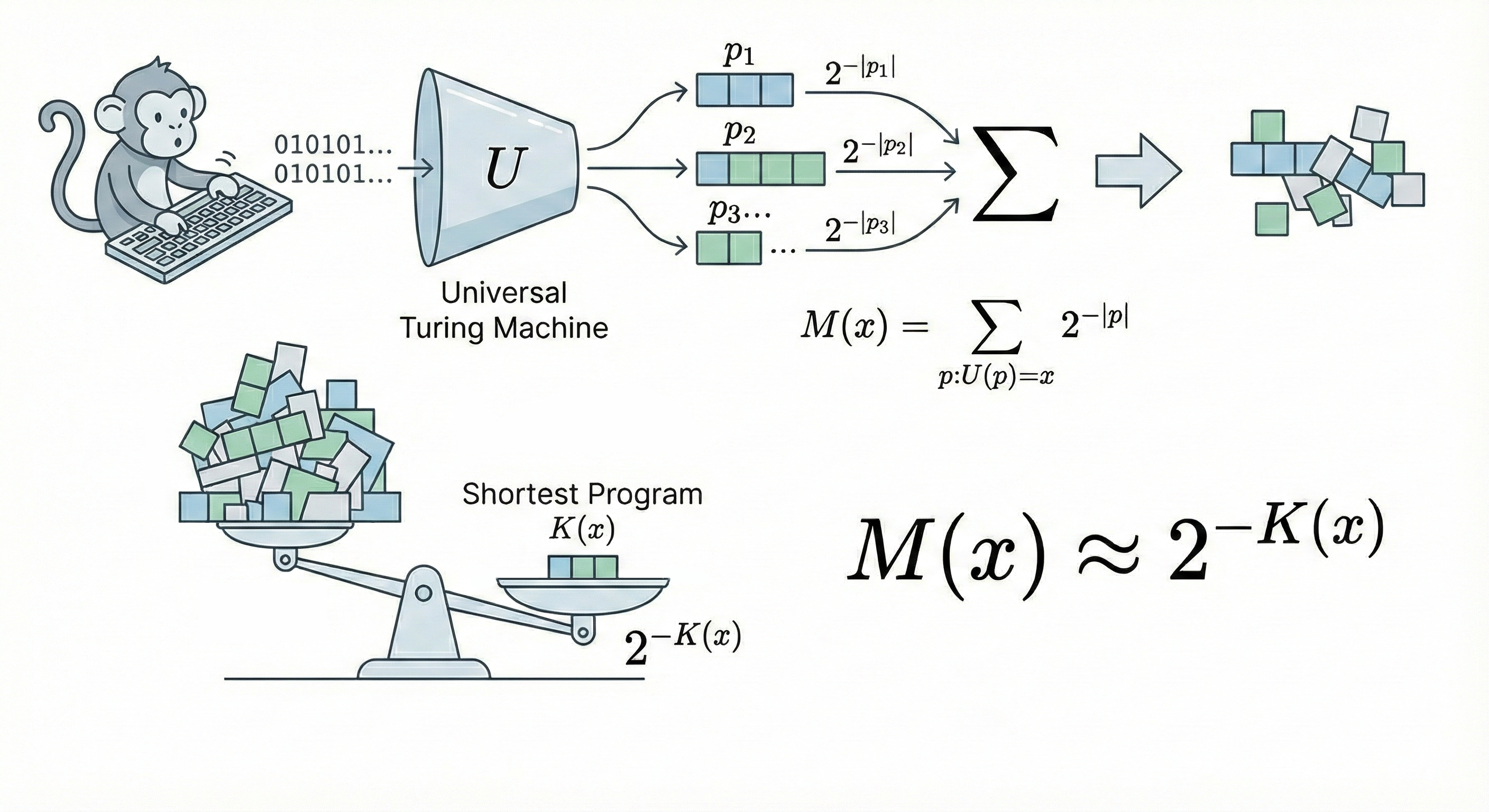
简单即真理,不是哲学,是数学。
使用算法概率,我们可以穷举图灵机,估算二维结构的复杂度
所罗门诺夫归纳 $\xi$:完美的预测机器
既然既然 $M(x)$ 给了我们数据的先验概率,所罗门诺夫顺水推舟,将其转化为预测模型。
他构想了一个终极预测器 $\xi$。既然我们不知道数据背后到底是哪种规律在起作用,那就把所有可能的、可计算的概率分布都拿来,组成一个集合 $\mathcal{M}$。每一个 $\nu \in \mathcal{M}$ 都是一种解释数据的「理论」或「假说」。
那么,怎么给这些理论分配权重呢?所罗门诺夫不需要重新发明轮子,他直接借用了 $M(x)$ 的结论:一个理论 $\nu$(本质上也是一段程序)在宇宙中存在的先验概率,正比于 $2^{-K(\nu)}$。
于是,诞生了所罗门诺夫归纳(Solomonoff Induction):
$$ \xi_U(x_{1:t}) = \sum_{\nu \in \mathcal{M}} w_\nu \nu(x_{1:t}), \quad \text{其中 } w_\nu = 2^{-K(\nu)} $$现在,我们可以清晰地看到这个公式并非拼凑,而是逻辑的必然流露:
- 求和 ($\sum$) —— 伊壁鸠鲁的坚持:这对应了算法概率中「对所有可能的程序求和」。我们不因为某个理论看起来奇怪就将其剔除,保留所有可能性。
- 权重 ($2^{-K}$) —— 奥卡姆的胜利:这并非人为设定的偏好,而是源于前文推导的算法概率。复杂的理论因为其描述程序长,自然而然地被赋予了极低的权重。
- 贝叶斯更新:随着数据 $x_{1:t}$ 的累积,$\xi$ 会自动筛选。那些预测错误的理论 $\nu$,其概率项 $\nu(x_{1:t})$ 会迅速归零;而那些**既简单($2^{-K}$ 大)又准确($\nu(x)$ 高)**的理论,将在求和中占据主导地位。
通用归纳:收敛的必然性
$\xi$ 最强大的地方在于它的通用性和收敛性。可以说,$\xi$ 和 $M$ 在数学上是殊途同归的($M(x) \overset{\times}{=} \xi(x)$)。这意味着,$\xi$ 继承了算法概率的所有性质。数学家已经证明了一个极为重要的收敛定理:
假设环境的真实分布是 $\mu$(只要它是可计算的),那么随着观测数据的增加,所罗门诺夫归纳 $\xi$ 的预测结果,将以极快的速度收敛到真实分布 $\mu$。
$$ \sum_{t=1}^{\infty} \mathbb{E} \left[ \sum_{x_t} \left(\xi(x_t|x_{\lt t}) - \mu(x_t|x_{\lt t}) \right)^2 \right] \le K(\mu) \ln 2 + \mathcal{O}(1) $$这个不等式告诉我们:预测的总误差是有上限的,这个上限仅取决于环境本身的复杂度 $K(\mu)$。
这就意味着,所罗门诺夫归纳是理论上最优的学习机器。 它不需要我们在神经网络架构、超参数上纠结,只要给它足够的数据,它就能自动找到隐藏在数据背后的那个「真实生成程序」,无论这个程序是牛顿力学,还是相对论,亦或是一套我们要到 3000 年才能发现的物理定律。
这就是通用归纳(Universal Induction)。它统一了归纳推理、模型选择和贝叶斯统计,成为了智能在数学上的终极定义。
三、现实的倒影:AIXI、大模型与科学的尽头
虽然 $\xi_U$ 和 $K(x)$ 包含了不可计算的成分,如同柏拉图理念世界中的完美原型,无法在物理世界直接构建。但如果我们观察 2025 年的 AI 进展,会发现许多突破性技术,其实都是这套理论在现实洞穴墙壁上的投影。
终极智能体 AIXI:从预测到决策
掌握了完美的预测工具 $\xi_U$,我们距离 AGI 只差最后一步:决策。
如果我们给 $\xi$ 加上一个目标(Reward),就诞生了理论上最强的通用强化学习智能体——AIXI。其决策公式如下:
$$ y_t := \arg\max_{y_t} \sum_{x_t} \dots \max_{y_n} \sum_{x_n} [r_t + \dots + r_n] M(x_{1:n} \mid y_{1:n}) $$这个公式描述了 AIXI 的思考过程:它利用通用分布 $M$ 来模拟未来所有可能的观测分支,预测在不同行动序列下,环境会如何反馈,然后选择那个能让未来累积奖励期望值最大的动作。AIXI 是智能的数学上限,它告诉我们:智能 = 强大的压缩、预测模型 + 奖励最大化策略。
压缩即学习:ARC-AGI 与 VAE 的本质
现实中,我们无法计算 $K(x)$,但我们一直在寻找它的近似解。
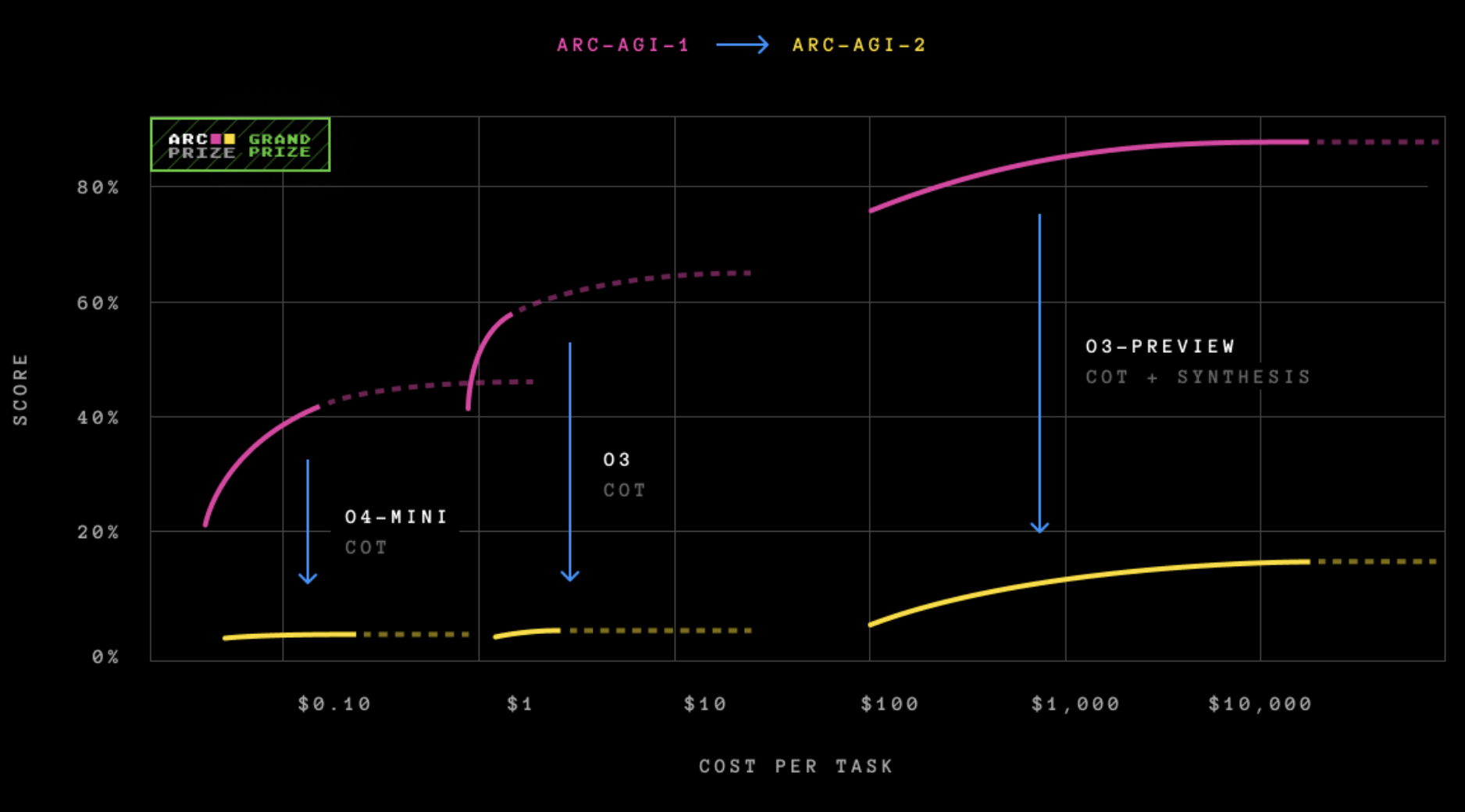
ARC-AGI 任务对于很多 LLM 来说仍然极为困难
Keras 之父 François Chollet 提出的 ARC-AGI 测试,因其极少的样本量和极高的推理难度,成为了检验 AI 是否具备「通用性」的试金石。传统的深度学习依赖海量数据,面对 ARC 往往束手无策。然而,基于「压缩」思想的方法却异军突起。
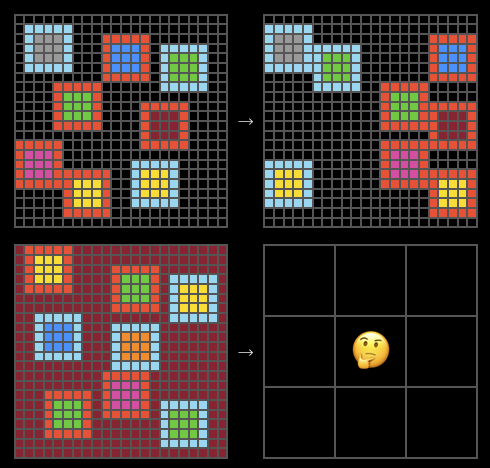
一个 ARC-AGI 任务
为了理解这一突破,我们需要回溯到一开始提到的那个「时间序列」的统一视角。
在 ARC 任务中,我们通常有几对示例(输入 $x$ 和输出 $y$),以及一个新的测试输入 $x_n$,目标是预测 $y_n$。如果我们把这个过程看作一个随时间流动的序列,那么现在的「历史数据」就是:
$$ D = (x_1, y_1, x_2, y_2, \dots, x_{n-1}, y_{n-1}, x_n) $$我们的任务,本质上就是预测序列的下一个元素 $y_n$。
利用所罗门诺夫归纳的框架,要预测 $y_n$,我们实际上是在寻找一个能最好地生成当前历史序列 $D$ 的理论 $\nu^*$。根据前文推导的公式,最优的理论 $\nu^*$ 必须同时满足两个条件:解释力强(概率大)且足够简单(复杂度低)。我们套用 $\xi_U$ 的公式,但为了简单,只寻找最优的那个 $\nu^*$:
$$ \nu^* = \arg\max_\nu \underbrace{2^{-K(\nu)}}_{\text{简单性}} \cdot \underbrace{\nu(D)}_{\text{解释力}} $$为了方便计算,我们对等式两边取负对数。原本的「最大化概率」问题,瞬间变成了一个我们熟悉的「最小化损失」问题:
$$ \text{Loss} = \underbrace{-\log_2 \nu(D)}_{\text{重构误差}} + \underbrace{K(\nu)}_{\text{模型复杂度}} $$看!这不仅仅是数学变换,这是物理意义的显现:
- 第一项 $-\log_2 \nu(D)$:这是重构误差。如果你的理论 $\nu$ 很糟糕,它就很难还原出历史数据 $(x_1, y_1 \dots)$,这项数值就会很大。
- 第二项 $K(\nu)$:这是模型复杂度。我们不仅要求模型能拟合数据,还要求模型本身的描述(代码长度或参数量)尽可能短。
两者加起来,恰恰就是最小描述长度(MDL)。
现在,让我们把目光投向现代生成模型——变分自编码器(VAE)。惊人的是,VAE 的损失函数(ELBO 的负值)几乎完美地复刻了这个结构:
- Reconstruction Loss:对应第一项,要求模型能准确还原输入数据。
- KL Divergence:对应第二项,约束隐变量的分布,本质上就是对模型复杂度的正则化项。
CompressARC 等前沿工作正是利用了这一点。它们不把 ARC 看作普通的分类问题,而是看作一个序列压缩问题。模型试图找到一个极其精简的潜在程序($z$),这个程序不仅能无损压缩(重构)所有的训练示例,还能自然地延伸到 $x_n$,从而「生成」出 $y_n$。

随着训练的深入,模型的描述长度逐渐降低,而预测也越来越符合要求。
这强有力地证明了 Ilya 的论断:学习的本质,就是在做有损压缩。 当你把一系列数据压缩到极致,剩下的那个「压缩包」(程序),就是智能本身。
灾难性遗忘的解药:求和的力量
所罗门诺夫归纳还为当今大模型的一个顽疾——灾难性遗忘,提供了理论解药。
在传统的模型训练中,我们通常只保留一个最优模型(参数组),这相当于我们只保留了 $\mathcal{M}$ 中概率最大的那个 $\nu^*$。然而,$\xi_U$ 的定义是 $\sum_{\nu}$。抛弃求和,是灾难性遗忘的根源。
当我们只保留一个模型时,面对新数据,如果新旧数据冲突,我们被迫修改参数,从而破坏了对旧数据的记忆。但在 $\xi_U$ 的框架下,如果新数据出现,我们只是重新计算不同理论 $\nu$ 的权重。旧的理论可能解释不了新数据,权重下降,但它依然存在;新的理论(可能更复杂)权重上升。
这解释了为什么 Ensemble Methods(集成方法) 和 MoE(混合专家模型) 如此有效。MoE 通过冻结部分专家、激活新专家,模拟了在不同理论间切换的过程。它保留了多种「解释世界的路径」,而非强行将世界压缩进单一的参数路径中。
科学共同体:人类就是 AGI
最后,如果我们将视野拉大,会发现整个人类科学发展的过程,本身就是一个巨大的 AGI 在运行所罗门诺夫归纳。
我们可以把科学界看作一个整体:
- $\mathcal{M}$ (理论池):每一位科学家提出的假说、理论,都是 $\mathcal{M}$ 中的一个 $\nu$。
- $x_{1:t}$ (数据):人类历史上观测到的所有实验数据。
- 学术机制:我们鼓励创新(提出新的 $\nu$),同时奖励准确性($\nu(x)$ 高)。
科学哲学家托马斯·库恩提出的「范式转换(Paradigm Shift)」,在数学上有了完美的对应。在反常数据(如水星近日点进动)出现前,牛顿力学作为一个极其简单($K$ 小)且相当准确的理论,拥有极高的权重。当反常数据出现,牛顿力学的预测概率 $\nu(x)$ 下降。此时,广义相对论虽然更复杂($K$ 大,初始权重低),但它能完美解释新数据。根据贝叶斯更新,相对论的权重逐渐超过牛顿力学,完成了范式转换。
从这个角度看,人类群体智能的演化,并不神秘,它忠实地遵循着所罗门诺夫写下的公式。
结语
在机器学习领域,有一个著名的「没有免费午餐定理」(NFL),声称如果没有先验假设,所有算法在所有问题上的平均表现是一样的。
但所罗门诺夫归纳打破了这个咒语。它拒绝了「所有世界出现的概率都一样」这种均匀假设。它基于一个极其本质的信念:我们所处的宇宙,是由简单的物理定律(短程序)支配的。
在这个假设下,偏好简单性的所罗门诺夫归纳,以及它的现实近似者——那些基于 Transformer、使用 SGD 优化的大模型,就是那顿免费的午餐。
站在 2025 年的回望中,Ilya Sutskever 的「压缩即智能」不再是一句口号,而是对这套古老理论的现代回响。当我们惊叹于 AI 的涌现能力时,不要忘记,这一切并非魔法,而是数学。那个关于压缩、预测与复杂度的公式,早已在几十年前,静静地预言了今天的一切。